Euclid's Proof of the Pythagorean Theorem

Euclid's proof of the Pythagorean theorem appears in Elements, Book I, Proposition 47.
Unlike Pythagoras's rearrangement method, it demonstrates the theorem by geometrically dissecting and rearranging the areas of the squares constructed on each side of a right triangle.

Figure 1. First configuration showing area equality between ACHI and ADNM.

Let us first examine the first figure.
Here, ∠ACB and ∠CMB are right angles, and ACHI, BCGF, and ABCE are all squares. △ACI has base $\overline{AC}$ and a corresponding height equal to $\overline{AC}$. Moreover, since ∠IAC and ∠ACB are right angles, $\overline{AI} \parallel \overline{CB}$. Therefore, the area of △ABI, calculated as base $\overline{AI}$ times height $\overline{AC}$, equals the area of △ACI.

△ABI and △ADC are congruent by SAS ($\overline{AI} = \overline{AC}$, $\overline{AB} = \overline{AD}$, included angle equal). Since △ACI and △ABI have the same area, △ACI and △ADC also have the same area. △ADC and △ADM share the same base $\overline{AD}$ and height, so their areas are equal. Hence, △ACI and △ADM also have the same area.

The area of square ACHI is twice that of △ACI, and the area of rectangle ADNM is twice that of △ADM. Therefore, these two quadrilaterals have equal areas.

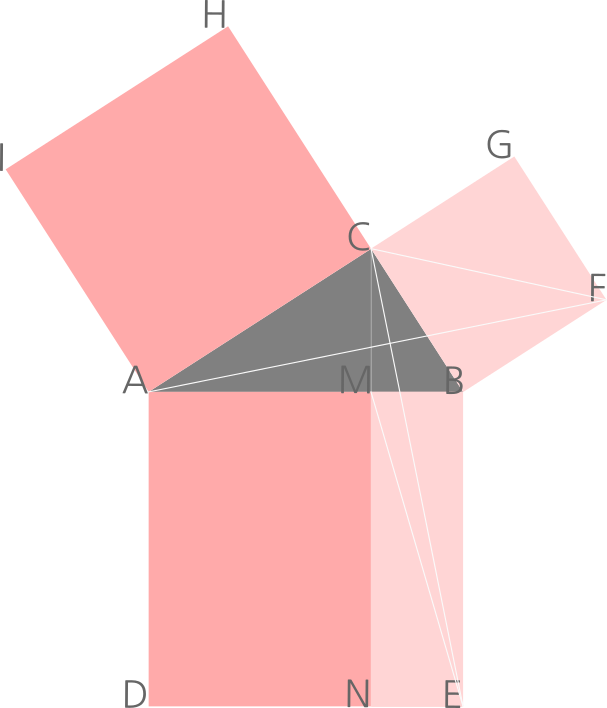
Figure 2. Second configuration showing area equality between BCGF and BENM.

The second figure illustrates the next part of the proof.
△BCF has base $\overline{BC}$ and its corresponding height. △BAF has base $\overline{BF}$, and since $\overline{BF} \parallel \overline{AC}$, △BCF and △BAF have equal areas.

△BAF and △BEC are congruent (∠ABF = ∠CBE, $\overline{BF} = \overline{BC}$, $\overline{BE} = \overline{BA}$), so their areas are equal. Since △BCF and △BAF have the same area, △BCF and △BEC also have the same area. △BEM, with base $\overline{BE}$, has the same area as △BEC.

The area of square BCGF is twice that of △BCF, and the area of rectangle BENM is twice that of △BEM. Therefore, these two quadrilaterals have equal areas.

In conclusion, the sum of the areas of squares ACIH and BCGF equals the area of square ADEB.
Let $\overline{AC} = a$, $\overline{BC} = b$, and $\overline{AB} = c$. Then:

$a^2 + b^2 = c^2$