Proof of the Sum of the Interior Angles of a Triangle Using Parallel Lines and Angle Properties

To prove that the sum of the interior angles of a triangle is 180°, the properties of parallel lines and the angles formed when they are intersected by a transversal are applied.

When two lines are parallel and a third line intersects them, the corresponding angles have equal measures, and the alternate interior angles also have equal measures. This property can be illustrated as follows:

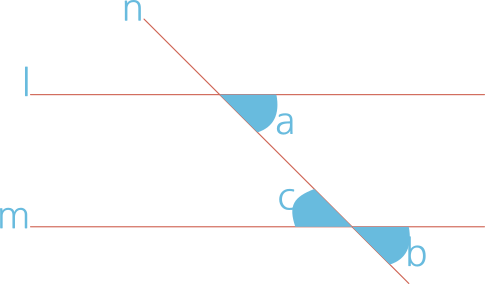
Figure 1. Corresponding and alternate angles formed when a transversal intersects parallel lines

As shown in the figure above, if lines (l) and (m) are parallel and are intersected by another line, the corresponding angles ∠a and ∠b are equal. Furthermore, since ∠b and ∠c are vertically opposite angles, they are also equal, which means that the alternate interior angles ∠a and ∠c are likewise equal.

In other words, when two parallel lines are intersected by another line, the corresponding angles are equal and the alternate interior angles are also equal. Conversely, if either the corresponding angles or the alternate interior angles are equal, the two lines can be determined to be parallel.

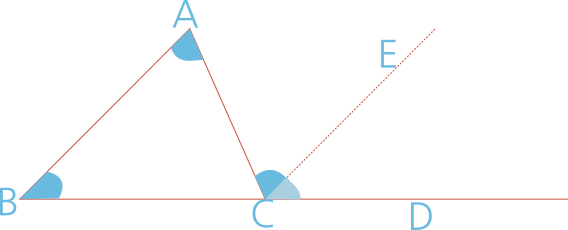
Figure 2. Construction of an auxiliary line parallel to one side of △ABC

The figure above shows △ABC with point D chosen arbitrarily on the extension of side BC, and an auxiliary line drawn through point C parallel to AB, on which point E is placed. Since AB and CE are parallel, the corresponding angles and the alternate interior angles are equal. Specifically, ∠BAC and ∠ACE are equal as alternate interior angles, and ∠ABC and ∠ECD are equal as corresponding angles.

Therefore, the sum of the interior angles of △ABC is equal to ∠ABC + ∠BAC + ∠ACB. Since ∠ABC is equal to ∠ECD and ∠BAC is equal to ∠ACE, the sum of the interior angles can be expressed as ∠ECD + ∠ACE + ∠ACB, which is 180°.