Published on

Leonardo da Vinci’s Proof of the Pythagorean Theorem

Authors
  • avatar
    Name
    hwahyeon
    Twitter
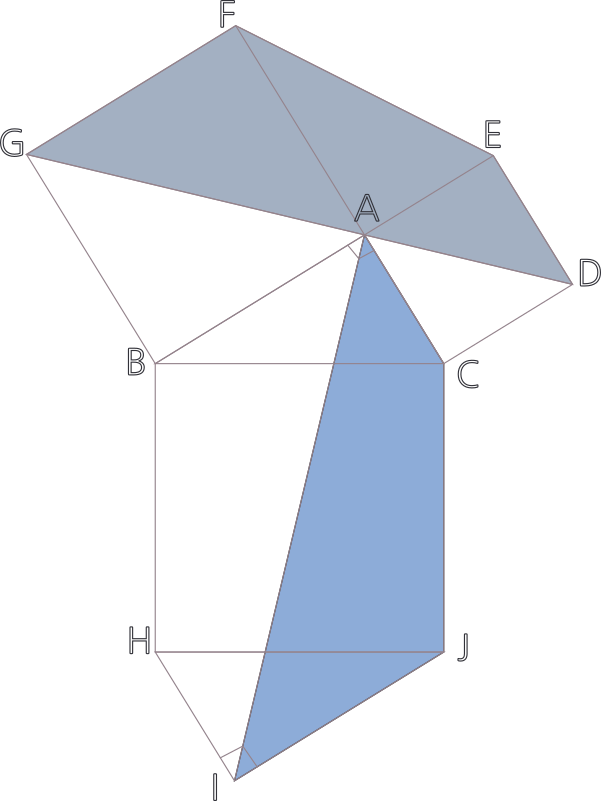
Figure 1

△IJH is congruent to triangle △ABC. By drawing auxiliary lines GD and AI, quadrilaterals DEFG, DCBG, IHBA, and ACJI each have the same area.

Thus, the hexagons BCDEFG and ABHIJC have equal areas.
Removing two copies of △ABC from each hexagon leaves the remaining areas equal.

That is:
BCDEFG−△AEF−△ABC=ABGF+ACDEBCDEFG - △AEF - △ABC = ABGF + ACDE
ABHIJC−△ABC−△IJH=BCJHABHIJC - △ABC - △IJH = BCJH

Therefore, ABGF+ACDE=BCJHABGF + ACDE = BCJH, which proves the Pythagorean theorem.

Discuss on Twitter • View on GitHub